Гиперболастические функции - Hyperbolastic functions - Wikipedia







В гиперболастические функции, также известный как модели гиперболастического роста, находятся математические функции которые используются в медицинских статистическое моделирование. Эти модели были первоначально разработаны для отражения динамики роста сфер многоклеточных опухолей и были представлены в 2005 году Мохаммадом Табатабаи, Дэвидом Уильямсом и Зораном Бурсаком.[1] Точность гиперболастических функций при моделировании проблем реального мира отчасти объясняется их гибкостью в точке перегиба.[1] Эти функции могут использоваться в широком спектре задач моделирования, таких как рост опухоли, стволовая клетка пролиферация, фармакокинетика, рост рака, функция активации сигмовидной кишки в нейронные сети и эпидемиологическое прогрессирование или регресс заболевания.[1][2][3]
В гиперболастические функции может моделировать кривые роста и спада, пока не достигнет грузоподъемность. Благодаря своей гибкости, эти модели находят широкое применение в медицине, с возможностью фиксировать прогрессирование заболевания с помощью промежуточного лечения. Как показывают цифры, гиперболастические функции может поместиться сигмоидальная кривая указывает на то, что самая низкая скорость наблюдается на ранней и поздней стадиях. В дополнение к сигмоидальной форме, он также может приспособиться к двухфазным ситуациям, когда медицинские вмешательства замедляют или обращают вспять прогрессирование заболевания; но когда эффект лечения исчезает, болезнь начинает вторую фазу своего развития, пока не достигнет своей горизонтальной асимптоты.
Одной из основных характеристик этих функций является то, что они не только соответствуют сигмоидальным формам, но также могут моделировать двухфазные модели роста, которые другие классические сигмоидальные кривые не могут адекватно моделировать. Эта отличительная особенность имеет преимущества в различных областях, включая медицину, биологию, экономику, инженерию и др. агрономия, и теория автоматизированных систем.[4][5][6][7][8]
Функция H1
В уравнение скорости гиперболастического типа I, обозначаемый H1, определяется как:
куда любое действительное число и численность населения . Параметр представляет собой грузоподъемность, а параметры и вместе представляют скорость роста. Параметр дает расстояние от симметричной сигмоидальной кривой. Решение уравнения скорости гиперболастики типа I для дает:
куда это обратный гиперболический синус функция. Если кто-то желает использовать начальное условие , тогда можно выразить как:
- .
Если , тогда сводится к:
- .
В гиперболастическая функция I типа обобщает логистическая функция. Если параметры , тогда это станет логистической функцией. Эта функция это гиперболастическая функция I типа. В стандартная гиперболастическая функция типа I является
- .
Функция H2
В уравнение скорости гиперболастического типа II, обозначаемый H2, определяется как:
куда это гиперболический тангенс функция это грузоподъемность, и оба и совместно определять скорость роста. Кроме того, параметр представляет собой ускорение во времени. Решение гиперболастической функции скорости типа II для дает:
- .
Если кто-то желает использовать начальное условие тогда можно выразить как:
- .
Если , тогда сводится к:
- .
В стандартная гиперболастическая функция II типа определяется как:
- .
Функция H3
Уравнение гиперболастической скорости типа III обозначается H3 и имеет вид:
- ,
куда > 0. Параметр представляет собой грузоподъемность, а параметры и совместно определять скорость роста. Параметр представляет собой ускорение шкалы времени, а размер представляет собой расстояние от симметричной сигмоидальной кривой. Решение дифференциального уравнения типа III:
- ,
с начальным условием мы можем выразить в качестве:
- .
Гиперболастическое распределение типа III представляет собой трехпараметрическое семейство непрерывных распределения вероятностей с масштабными параметрами > 0 и ≥ 0 и параметр как параметр формы. Когда параметр = 0 гиперболастическое распределение III типа сводится к распределение Вейбулла.[9] Гиперболастический кумулятивная функция распределения типа III определяется:
- ,
и соответствующий функция плотности вероятности является:
- .
В функция опасности (или частота отказов) определяется как:
В функция выживания дан кем-то:
Стандартная гиперболастическая кумулятивная функция распределения типа III определяется как:
- ,
и соответствующая ему функция плотности вероятности:
- .
Характеристики
Если кто-то желает вычислить точку где популяция достигает процента своей вместимости , то можно решить уравнение:
за , куда . Например, половину точки можно найти, задав .
Приложения

По словам исследователей стволовых клеток из Института регенеративной медицины Макгоуэна при Университете Питтсбурга, «новая модель [называемая гиперболастическим типом III или] H3 является дифференциальное уравнение это также описывает рост клеток. Эта модель допускает гораздо больше вариаций и, как было доказано, лучше предсказывает рост ".[10]
Модели гиперболастического роста H1, H2 и H3 были применены для анализа роста твердых тел. Карцинома Эрлиха используя различные методы лечения.[11]
В зоотехнике[12] гиперболастические функции были использованы для моделирования роста цыплят-бройлеров.[13] Гиперболастическая модель III типа использовалась для определения размера восстанавливающейся раны.[14]
В области заживления ран гиперболастические модели точно отображают ход заживления. Такие функции использовались для исследования вариаций скорости заживления различных видов ран и на разных этапах процесса заживления, принимая во внимание области микроэлементов, факторов роста, диабетических ран и питания.[15][16]
Другое применение гиперболастических функций находится в области стохастическая диффузия процесс, функция среднего которого является гиперболастической кривой типа I. Изучены основные характеристики процесса и оценка максимального правдоподобия для параметров процесса.[17]С этой целью применяется алгоритм метаэвристической оптимизации светлячка после ограничения параметрического пространства поэтапной процедурой. Некоторые примеры, основанные на смоделированных примерах путей и реальных данных, иллюстрируют это развитие. Образец пути диффузионный процесс моделирует траекторию частицы, погруженной в текущую жидкость и подвергающейся случайным смещениям из-за столкновений с другими частицами, что называется Броуновское движение.[18][19][20][21] Гиперболастическая функция типа III была использована для моделирования пролиферации взрослых мезенхимальный и эмбриональные стволовые клетки;[22][23][24][25] и гиперболастическая смешанная модель типа II использовалась при моделировании рак шейки матки данные.[26] Гиперболастические кривые могут быть важным инструментом при анализе клеточного роста, подбора биологических кривых и роста клеток. фитопланктон.[27][28]
В экология леса и управления, гиперболастические модели были применены для моделирования взаимосвязи между DBH и высотой.[29]
Многопараметрическая гиперболастическая модель III типа был использован для анализа динамики роста фитопланктона с учетом концентрации питательных веществ.[30]
Гиперболастические регрессии
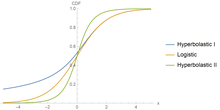
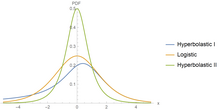
Гиперболастические регрессии находятся статистические модели которые используют стандартные гиперболические функции моделировать дихотомический переменная результата. Цель бинарной регрессии - предсказать двоичную исходную (зависимую) переменную с использованием набора независимых (независимых) переменных. Двоичная регрессия обычно используется во многих областях, включая медицину, здравоохранение, стоматологию и биомедицину. Бинарный регрессионный анализ использовался для прогнозирования эндоскопический поражения при дефиците железа анемия.[31] Кроме того, для различения злокачественных и доброкачественных заболеваний применялась бинарная регрессия. придаточная масса до операции.[32]
Гиперболастическая регрессия I типа
Позволять быть двоичной выходной переменной, которая может принимать одно из двух взаимоисключающих значений: успех или неудача. Если мы закодируем успех как и неудача как вероятность гиперболастического успеха I типа как функция объясняющие переменные дан кем-то:
- ,
куда параметры модели. Шансы на успех - это отношение вероятности успеха к вероятности неудачи. Для гиперболастической регрессии типа I шансы на успех обозначены и выражается уравнением:
- .
Логарифм называется логит гиперболастики типа I. Преобразование логита обозначается через и может быть записано как:
- .
Гиперболастическая регрессия II типа
Для двоичной выходной переменной вероятность гиперболастического успеха типа II как функция объясняющие переменные является:
- ,
Для гиперболастической регрессии типа II шансы на успех обозначены и определяется:
Преобразование логита обозначается и определяется:
Рекомендации
- ^ а б c Табатабай, Мохаммад; Уильямс, Дэвид; Бурсац, Зоран (2005). «Модели гиперболастического роста: теория и применение». Теоретическая биология и медицинское моделирование. 2: 14. Дои:10.1186/1742-4682-2-14. ЧВК 1084364. PMID 15799781.
- ^ Q. Эштон Актон П. Клетки - достижения в исследованиях и применении. [Интернет]. Атланта: ScholarlyMedia LLC; 2012 [цитируется 27 апреля 2020 г.]. Доступна с: https://public.ebookcentral.proquest.com/choice/publicfullrecord.aspx?p=4973379
- ^ Wadkin, L.E .; Orozco-Fuentes, S .; Неганова, И .; Лако, М .; Паркер, Н.Г .; Шукуров, А. (2020). «Введение в математическое моделирование ИПСК». Последние достижения в технологии ИПСК. 5.
- ^ Нейсенс, Патрисия; Мессенс, Вини; Геверс, Дирк; Качели, Жан; Де Вюист, Люк (2003). «Двухфазная кинетика роста и продукции бактериоцина с Lactobacillus amylovorus DCE 471 происходит в стрессовых условиях». Микробиология. 149 (4): 1073–1082. Дои:10.1099 / мик.0.25880-0. PMID 12686649.
- ^ Чу, Шарлин; Хан, Кристина; Симидзу, Хироми; Вонг, Бонни (2002). «Влияние фруктозы, галактозы и глюкозы на индукцию β-галактозидазы в кишечная палочка" (PDF). Журнал экспериментальной микробиологии и иммунологии. 2: 1–5.
- ^ Табатабай, М. А .; Eby, W. M .; Сингх, К. П .; Бэ, С. (2013). «Т-модель роста и ее применение в системах опухолевой иммунодинамики». Математические биологические науки и инженерия. 10 (3): 925–938. Дои:10.3934 / mbe.2013.10.925. ЧВК 4476034. PMID 23906156.
- ^ Пармун, Гасем; Мусави, Сейед; Поштдар, Адель; Сиадат, Сейед (2020). «Влияние токсичности кадмия на прорастание семян кунжута объясняется различными нелинейными моделями роста». Масличные и жиры, культуры и липиды. 27 (57). Дои:10.1051 / окл / 2020053.
- ^ Теория компьютерных систем - ЕВРОКАСТ 2019. Конспект лекций по информатике. 12013. 2020. Дои:10.1007/978-3-030-45093-9. ISBN 978-3-030-45092-2.
- ^ Камар Ш., Мсаллам Б.С. Сравнительное исследование между методами обобщенной максимальной энтропии и Байеса для оценки четырехпараметрической модели роста Вейбулла. Журнал вероятности и статистики. 2020 14 января; 2020: 1–7.
- ^ Рорс Т., Богдан П., Гараибех Б. и др. (нет данных). «Пролиферативная гетерогенность популяций стволовых клеток». Лаборатория визуализации живых клеток, Институт регенеративной медицины Макгоуэна. Цитировать журнал требует
| журнал =(помощь) - ^ Эби, Уэйн М .; Табатабай, Мохаммад А .; Бурзак, Зоран (2010). «Гиперболастическое моделирование роста опухоли при комбинированном лечении йодацетатом и диметилсульфоксидом». BMC Рак. 10: 509. Дои:10.1186/1471-2407-10-509. ЧВК 2955040. PMID 20863400.
- ^ Франция, Джеймс; Кебреаб, Эрмиас, ред. (2008). Математическое моделирование в питании животных. Уоллингфорд: КАБИ. ISBN 9781845933548.
- ^ Ahmadi, H .; Моттагиталаб, М. (2007). «Гиперболастические модели как новый мощный инструмент для описания кинетики роста бройлеров». Птицеводство. 86 (11): 2461–2465. Дои:10.3382 / пс.2007-00086. PMID 17954598.
- ^ Чхве, Тэён; Чин, Сонга (2014). «Новый синтез восстановления лицевых ран в реальном времени с использованием подповерхностного рассеяния». Научный мировой журнал. 2014: 1–8. Дои:10.1155/2014/965036. ЧВК 4146479. PMID 25197721.
- ^ Tabatabai, M.A .; Eby, W.M .; Сингх, К. (2011). «Гиперболастическое моделирование заживления ран». Математическое и компьютерное моделирование. 53 (5–6): 755–768. Дои:10.1016 / j.mcm.2010.10.013.
- ^ Ко, Унг Хён; Чой, Чонджин; Чоун, Джинсын; Луна, Сунгван; Шин, Дженнифер Х. (2019). «Физико-химически настроенные миофибробласты для стратегии заживления ран». Научные отчеты. 9 (1): 16070. Bibcode:2019НатСР ... 916070K. Дои:10.1038 / s41598-019-52523-9. ЧВК 6831678. PMID 31690789.
- ^ Баррера, Антонио; Роман-Роман, Патрисия; Торрес-Руис, Франсиско (2020). «Процессы диффузии для моделей, основанных на Вейбулле». Теория компьютерных систем - ЕВРОКАСТ 2019. Конспект лекций по информатике. 12013. С. 204–210. Дои:10.1007/978-3-030-45093-9_25. ISBN 978-3-030-45092-2.
- ^ Баррера, Антонио; Роман-Роман, Патрисия; Торрес-Руис, Франциско (2018). «Гиперболастический процесс диффузии типа I: оценка параметров с помощью алгоритма светлячка». Биосистемы. 163: 11–22. Дои:10.1016 / j.biosystems.2017.11.001. PMID 29129822.
- ^ Баррера, Антонио; Роман-Роан, Патрисия; Торрес-Руис, Франсиско (2020). «Гиперболастический процесс диффузии типа III: получение из обобщенного диффузионного процесса Вейбулла». Математические биологические науки и инженерия. 17 (1): 814–833. Дои:10.3934 / mbe.2020043. PMID 31731379.
- ^ Баррера, Антонио; Роман-Роман, Патрисия; Торрес-Руис, Франсиско (2020). «Два стохастических дифференциальных уравнения для моделирования поведения осцилляболастического типа». Математика. 8 (2): 155. Дои:10.3390 / math8020155.
- ^ Случайные процессы с приложениями. 2019. Дои:10.3390 / books978-3-03921-729-8. ISBN 978-3-03921-729-8.
- ^ Табатабай, Мохаммад А .; Бурзак, Зоран; Эби, Уэйн М .; Сингх, Каран П. (2011). «Математическое моделирование пролиферации стволовых клеток». Медицинская и биологическая инженерия и вычисления. 49 (3): 253–262. Дои:10.1007 / s11517-010-0686-у. PMID 20953843.
- ^ Эби, Уэйн М .; Табатабай, Мохаммад А. (2014). «Методы математического моделирования стволовых клеток». Терапевтическое применение при заболеваниях и травмах. Стволовые клетки и раковые стволовые клетки. 12. С. 201–217. Дои:10.1007/978-94-017-8032-2_18. ISBN 978-94-017-8031-5.
- ^ Wadkin, L.E .; Orozco-Fuentes, S .; Неганова, И .; Лако, М .; Шукуров, А .; Паркер, Н. Г. (2020). «Последние достижения в математическом моделировании плюрипотентных стволовых клеток человека». SN Прикладные науки. 2 (2). Дои:10.1007 / s42452-020-2070-3.
- ^ Стволовые клетки и раковые стволовые клетки, том 12. Стволовые клетки и раковые стволовые клетки. 12. 2014. Дои:10.1007/978-94-017-8032-2. ISBN 978-94-017-8031-5.
- ^ Табатабай, Мохаммад А .; Кенгвунг-Кеумо, Жан-Жак; Эби, Уэйн М .; Пэ, Седжонг; Guemmegne, Juliette T .; Манн, Апендер; Фуад, Мона; Куропатка, Эдвард Э .; Сингх, Каран П. (2014). «Различия в показателях смертности от рака шейки матки, определенные с помощью модели типа II со смешанными эффектами продольной гиперболастики». PLOS ONE. 9 (9): e107242. Bibcode:2014PLoSO ... 9j7242T. Дои:10.1371 / journal.pone.0107242. ЧВК 4167327. PMID 25226583.
- ^ Вериссимо, Андре; Paixão, Laura; Невес, Ана; Винга, Сусана (2013). «BGFit: Управление и автоматическое построение кривых биологического роста». BMC Bioinformatics. 14: 283. Дои:10.1186/1471-2105-14-283. ЧВК 3848918. PMID 24067087.
- ^ Табатабай, М. А .; Eby, W. M .; Bae, S .; Сингх, К. П. (2013). «Гибкая многовариантная модель роста фитопланктона». Математические биологические науки и инженерия. 10 (3): 913–923. Дои:10.3934 / mbe.2013.10.913. PMID 23906155.
- ^ Эби, Уэйн М .; Oyamakin, Samuel O .; Чукву, Анджела У. (2017). «Новая нелинейная модель, примененная к зависимости высоты от DBH в Gmelina arborea». Экология и управление лесами. 397: 139–149. Дои:10.1016 / j.foreco.2017.04.015.
- ^ Табатабай, М. А .; Eby, W. M .; Bae, S .; Сингх, К. П. (2013). «Гибкая многовариантная модель роста фитопланктона». Математические биологические науки и инженерия. 10 (3): 913–923. Дои:10.3934 / mbe.2013.10.913. PMID 23906155.
- ^ Маджид, Шахид; Салих, Мохаммад; Васая, Розина; Джафри, Васим (2008). «Предикторы поражения желудочно-кишечного тракта при эндоскопии при железодефицитной анемии без желудочно-кишечных симптомов». BMC Гастроэнтерология. 8: 52. Дои:10.1186 / 1471-230X-8-52. ЧВК 2613391. PMID 18992171.
- ^ Тиммерман, Дирк; Testa, Antonia C .; Борн, Том; Феррацци, Энрико; Амей, Ливеке; Konstantinovic, Maja L .; Ван Калстер, Бен; Коллинз, Уильям П .; Вергота, Игнас; Ван Хаффель, Сабина; Валентин, Лил (2005). «Модель логистической регрессии для различения доброкачественных и злокачественных образований придатков перед операцией: многоцентровое исследование Международной группы анализа опухолей яичников». Журнал клинической онкологии. 23 (34): 8794–8801. Дои:10.1200 / JCO.2005.01.7632. PMID 16314639.




























































